南开大学付浩浩/邵学广课题组近期在Nature Computational Science杂志上发表了题为《A formally exact method for high-throughput absolute binding-free-energy calculations》的研究成果[1]，通讯作者为南开大学付浩浩副研究员，第一作者为南开大学博士生卞恒伟。该研究首次提出了Lucid Double Decoupling Method（LDDM）方法，为解决绝对结合自由能计算中的效率问题提供了新方案。

在计算机辅助药物设计领域，准确计算蛋白质-配体结合自由能一直被视为圣杯。自1986年Hermans和Shankar

首次提出通过施加几何约束加快结合自由能计算收敛性并通过后处理计算约束贡献的方法以来，众多课题组相继发展了理论严谨的绝对结合自由能计算方法。近20年来，这些方法在药物设计、生物化学和物理化学研究领域得到了广泛应用。

然而，经典的基于FEP的双解耦法（DDM）如图1A所示，需要进行多步FEP计算，计算周期长、成本高，严重制约了绝对结合自由能在高通量筛选中的发展与应用。为解决这一瓶颈问题，付浩浩课题组提出的LDDM方法通过构建全新的热力学循环，并采用“0受力策略”减小FEP计算中的扰动，真正实现了微扰，从而极大程度上降低了计算绝对结合自由能的成本。

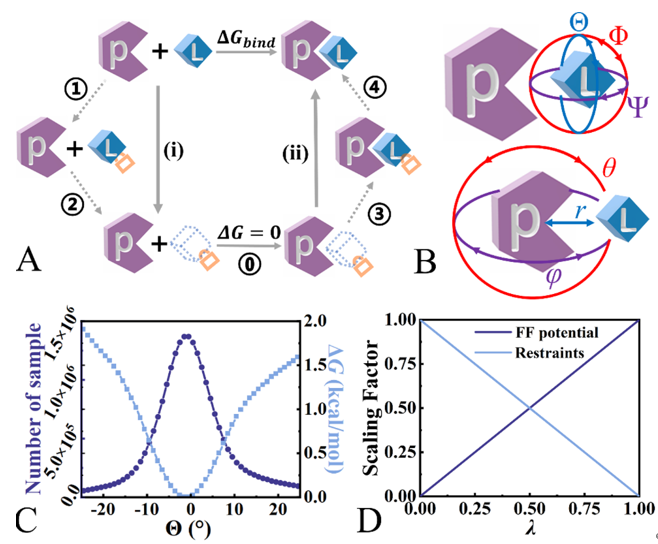
图1. LDDM策略示意图。

LDDM方法的核心创新在于设计了一种全新的热力学循环（如图1A实线所示），显著降低了蛋白质-配体相对运动，从而减少了系统扰动。在传统的DDM方法中，最耗时的步骤是在结合位点消失/生长配体，随着该过程的进行，蛋白-配体间相互作用有较大变化，因此体系扰动较大。而LDDM的关键策略是在配体消失/生长的同时生长/消失几何约束，使力场力与几何约束力相互抵消，体系在关键自由度上受力为零，即蛋白-配体在这些自由度上不存在相对运动，从而使体系扰动最小化，如图1B,1C,1D所示。

实验结果表明，零受力路径在整个模拟过程中保持了球面坐标和欧拉角方向运动模式的稳定性（如图2C所示），而如图2A, 2B所示传统DDM方法在约束生长-消失过程中在这些自由度方向上表现出较大的波动性。通过这一策略，LDDM方法比传统DDM方法提高了约四倍的计算效率。进一步将这一策略与双向采样(DWS)和氢质量重分配(HMR)算法相结合，最终实现了约八倍的效率提升（如表1所示）。

表1. LDDM和传统DDM模拟时间的对比。

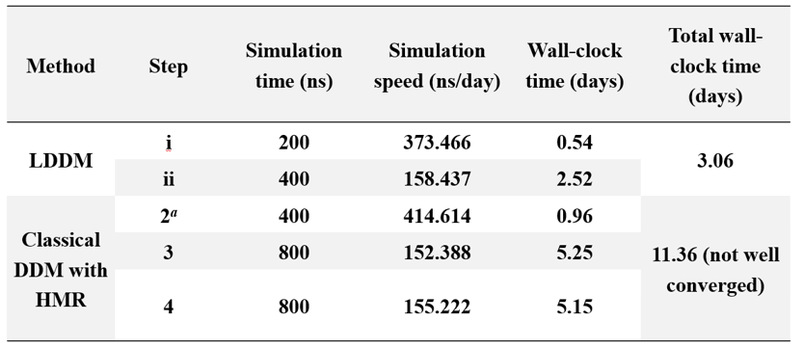
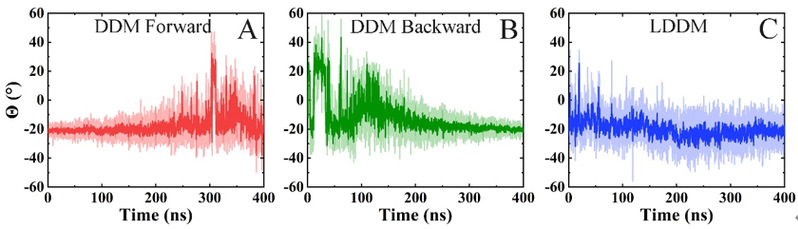
图2. DDM和LDDM约束生长-消失的过程中欧拉角上的运动模式变化。

为验证LDDM方法的准确性，该研究对45个已验证力场准确性的复合物（包括42个蛋白质-有机小分子和3个蛋白质-多肽体系）进行了绝对结合自由能计算。计算结果与实验值的平均无符号误差为0.7 kcal mol⁻¹，相关性达0.96，充分证明了LDDM方法的高准确性（如图3所示）。此外，对于结合过程中构象变化较大的肽类配体，通过额外的平均力势（PMF）计算增强了构象采样，仅增加不到5%的模拟时间，就确保了蛋白质-肽段复合物结合自由能计算的准确性。

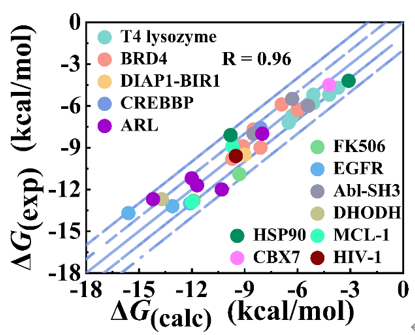
图3：蛋白质-配体结合自由能的实验值与计算值相关性。

为进一步展示LDDM方法的优势，对11个极具挑战性的复合物进行了绝对结合自由能计算（如图4所示）。与Schrödinger公司的FEP+相比较，对于P38-配体复合物，LDDM方法在显著减少模拟时间的同时（如表1所示），大幅提高了自由能计算的准确性（平均无符号误差：1.7 vs 5.3 kcal mol-1）。对于因蛋白质结构变化而收敛困难的PTP1B复合物，LDDM实现了4.8 kcal mol-1的平均无符号误差，明显优于Schrödinger的FEP+计算结果（11.6 kcal mol-1）。

表2. 不同方法的模拟时间。

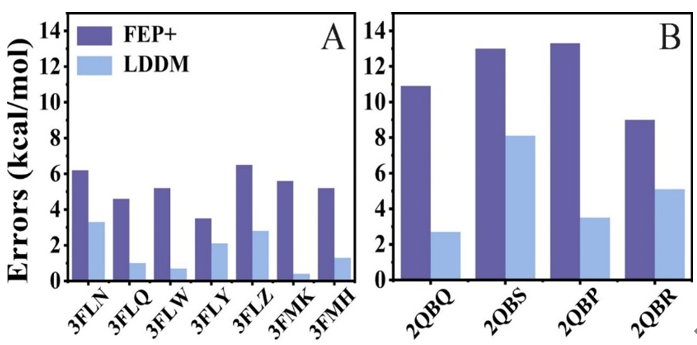
图4. 复杂体系绝对结合自由能计算的绝对误差。

该研究提出的LDDM方法在保持理论严谨性的同时，通过创新的热力学循环和零受力路径设计，显著提高了绝对结合自由能计算的效率和准确性，为计算化学、生物化学和药物化学研究提供了强大的工具。目前所有方法已经开源，读者可以在此链接（https://github.com/fhh2626/BFEE2）下载BFEE3软件，进行使用，相关教程可查询参考文献1中补充材料部分。

参考文献：

[1] Bian, H., Shao, X., Chipot, C. Cai, W., Fu, H*. A formally exact method for high-throughput absolute binding-free-energy calculations. Nat Comput Sci (2025). https://doi.org/10.1038/s43588-025-00821-w.